算法数学理论—梯度下降实现逻辑回归

Posted on

1.原始数据

1
2
3
4
5
6
7
8
9
10
11
#三大件
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os

path = 'data' + os.sep + 'LogiReg_data.txt'
# txt 没有header，手动指定
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
print("输出前五行数据：\n",pdData.head())
print("\n 数据维度：",pdData.shape)
1
2
3
4
5
6
7
8
9
10
11
12
positive = pdData[pdData['Admitted'] == 1]
negative = pdData[pdData['Admitted'] == 0]
# 指定画图域-长和宽
fig,ax = plt.subplots(figsize=(10,5))
# 散点图
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
# 设置图例
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

2.实现方案

  • 目标：建立分类器（求解出三个参数 𝜃0𝜃1𝜃2）

  • 设定阈值，根据阈值判断录取结果

    要完成的模块

    • sigmoid : 映射到概率的函数

    • model : 返回预测结果值

    • cost : 根据参数计算损失

    • gradient : 计算每个参数的梯度方向

    • descent : 进行参数更新

    • accuracy: 计算精度

3.具体实现

3.1 sigmoid

1
2
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

3.2 预测模型-数值运算转换成矩阵运算

1
2
def model(X, theta):
    return sigmoid(np.dot(X, theta.T))

3.3 数据准备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 添加一列𝜃0，指定是1
pdData.insert(0, 'Ones', 1) 
# 转成二维
orig_data = pdData.as_matrix()
# 获取列数
cols = orig_data.shape[1]
# 1 x1 x2
X = orig_data[:,0:cols-1]
# 标签
y = orig_data[:,cols-1:cols]

# 构造1行3列的theta
theta = np.zeros([1, 3])
print(X.shape,y.shape,theta.shape)
结果输出：(100, 3) (100, 1) (1, 3)

3.4 损失函数

  • 将对数似然函数去负号

    𝐷(ℎ𝜃(𝑥),𝑦)=−𝑦log(ℎ𝜃(𝑥))−(1−𝑦)log(1−ℎ𝜃(𝑥))

1
2
3
4
5
6
7
def cost(X, y, theta):
    left = np.multiply(-y, np.log(model(X, theta)))
    right = np.multiply(1 - y, np.log(1 - model(X, theta)))
    return np.sum(left - right) / (len(X))
    
print(cost(X, y, theta))
结果输出：0.6931471805599453

3.5 计算梯度

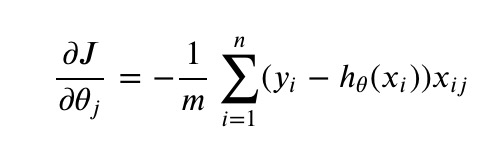
image

1
2
3
4
5
6
7
8
9
def gradient(X, y, theta):
    grad = np.zeros(theta.shape)
    # 外面符号提到括号里
    error = (model(X, theta)- y).ravel()
    #for each parmeter
    for j in range(len(theta.ravel())): 
        term = np.multiply(error, X[:,j])
        grad[0, j] = np.sum(term) / len(X)   
    return grad
  • 3中不同梯度下降方法
1
2
3
4
5
6
7
8
9
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2

def stopCriterion(type, value, threshold):
    #设定三种不同的停止策略
    if type == STOP_ITER:        return value > threshold
    elif type == STOP_COST:      return abs(value[-1]-value[-2]) < threshold
    elif type == STOP_GRAD:      return np.linalg.norm(value) < threshold
1
2
3
4
5
6
7
8
import numpy.random
# 洗牌打乱顺序
def shuffleData(data):
    np.random.shuffle(data)
    cols = data.shape[1]
    X = data[:, 0:cols-1]
    y = data[:, cols-1:]
    return X, y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import time

def descent(data, theta, batchSize, stopType, thresh, alpha):
    #梯度下降求解
    
    init_time = time.time()
    i = 0 # 迭代次数
    k = 0 # batch
    X, y = shuffleData(data)
    grad = np.zeros(theta.shape) # 计算的梯度
    costs = [cost(X, y, theta)] # 损失值

    
    while True:
        grad = gradient(X[k:k+batchSize], y[k:k+batchSize], theta)
        k += batchSize #取batch数量个数据
        if k >= n: 
            k = 0 
            X, y = shuffleData(data) #重新洗牌
        theta = theta - alpha*grad # 参数更新
        costs.append(cost(X, y, theta)) # 计算新的损失
        i += 1 

        if stopType == STOP_ITER:       value = i
        elif stopType == STOP_COST:     value = costs
        elif stopType == STOP_GRAD:     value = grad
        if stopCriterion(stopType, value, thresh): break
    
    return theta, i-1, costs, grad, time.time() - init_time

3.6 计算精度

1
2
3
4
5
6
7
8
9
10
11
#设定阈值
def predict(X, theta):
    return [1 if x >= 0.5 else 0 for x in model(X, theta)]
    
scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))
结果输出：accuracy = 89%